Derste göstermek üzere birkaç örnek karıştırırken önüme 2008 yılında Nature’da yayınlanmış ilginç bir makale denk geldi (linki http://www.nature.com/nature/journal/v456/n7218/full/nature07331.html).
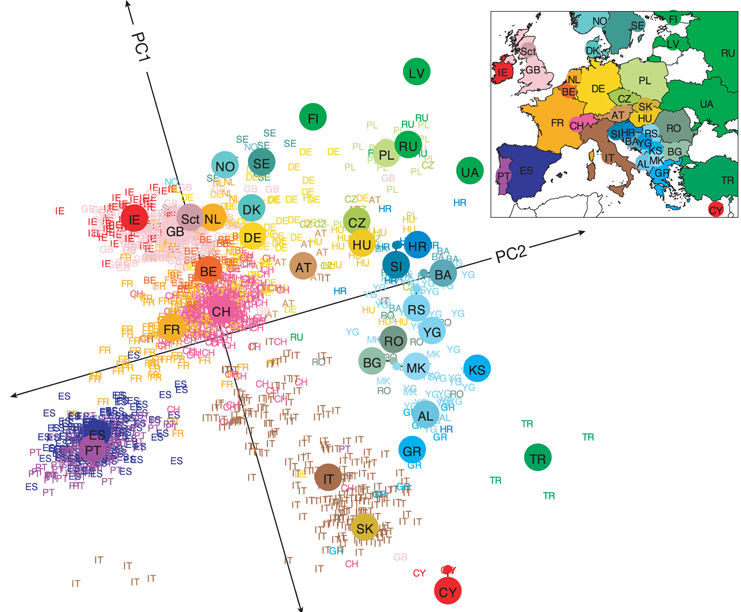
Özetle 3000 kadar Avrupalının genetik farklılıklarını bir şekilde sayısal olarak ifade edip (p tane değişkenle ya da bir başka deyişle p uzunluğunda bir vektörle) daha sonra veri madenciliğinde veri boyutunu küçültmek (dimensionality reduction) için kullanılan klasik yöntemlerden biri olan temel bileşen analizi,TBA (principal component analysis, PCA) ile iki boyuta indirgemişler ve bunu da harita üzerinde göstermişler. Her gördüğünüz nokta bir insanı temsil ediyor ve renkler ve kısaltmalar ile ülkeler belirlenmiş.
Ülkelerin yakınlığıyla genetik benzerlik arasındaki ilişki beklendik bir çıktı aslında. Burada koordinat sistemi (temel bileşen analizi kullanılarak iki boyuta indirilmiş koordinatlardaki gösterim) haritayla benzerlik kurmak adına döndürülmuş vaziyette. Büyük noktalar örneklerin ağırlık merkezini göstermekte. O ülke icin temsilci nokta gibi düşünebilirsiniz. Türkiye’den çok fazla örnek yok maalesef. Sebebi yapılan örneklem (sampling) ile alakalı bir durum olabileceği gibi, Türklerin böyle bir bilgiyi paylaşmaması da olabilir. Bir takım bulgular tahmin edilebilecek (ya da bilinenlerle) örtüşüyor. Gözüme çarpan Slovakların İtalyanlar ile yakınlığı ama bunun sebebi de Slovak tarafında örnek sayısının az olması büyük ihtimal ile.
ülke kodları (Maalesef İngilizce)- > AL, Albania; AT, Austria; BA, Bosnia-Herzegovina; BE, Belgium; BG, Bulgaria; CH, Switzerland; CY, Cyprus; CZ, Czech Republic; DE, Germany; DK, Denmark; ES, Spain; FI, Finland; FR, France; GB, United Kingdom; GR, Greece; HR, Croatia; HU, Hungary; IE, Ireland; IT, Italy; KS, Kosovo; LV, Latvia; MK, Macedonia; NO, Norway; NL, Netherlands; PL, Poland; PT, Portugal; RO, Romania; RS, Serbia and Montenegro; RU, Russia, Sct, Scotland; SE, Sweden; SI, Slovenia; SK, Slovakia; TR, Turkey; UA, Ukraine; YG, Yugoslavia.)
Güzel bir uygulama olmuş ve sonuçları da ilginç sayılır.
Temel Bileşen Analizi (TBA) nedir?
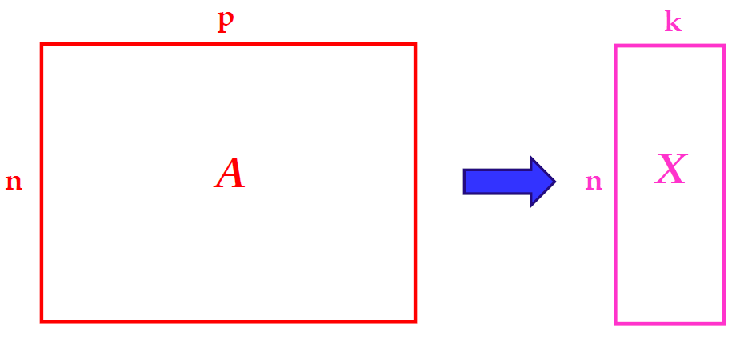
Kısaca TBA, p boyutlu bir uzaydan (verinizin p tane değişken ile ifade edildiğini düşünürseniz) k<p boyutlu bir uzaya dönüşümü sağlıyor. Şekil ile gösterecek olursak şöyle:
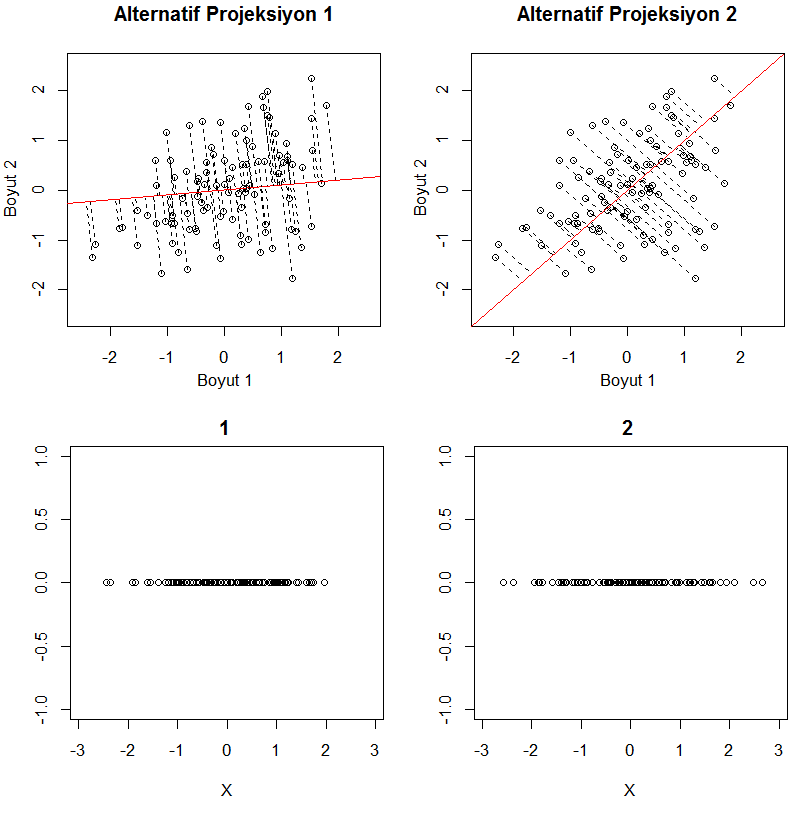
Bu küçülmeyi sağlamanın bir yolu verinizin daha küçük bir uzayda izdüşümünü (projeksiyon) almak. Aşağıda bunun geometrik olarak ne anlama geldiğini şekille anlatmaya çalıştım. Gösterim kolaylığı olması açısından 2 değişkenli 100 tane örnek içeren bir veri kullandım. Kırmızı ile gösterilen çizgi noktaların izdüşümünü alacağımız doğrular olsun. Aşağıda verinin bu doğrulardaki izdüşümünü yatay olarak döndürülmüş halini göstermeye çalıştım. Görülebileceği üzere sonsuz tane doğru üzerinde izdüşümü alabiliriz. Bu noktada hangi doğru/doğruları kullanmak en mantıklıdır sorusu akla geliyor.
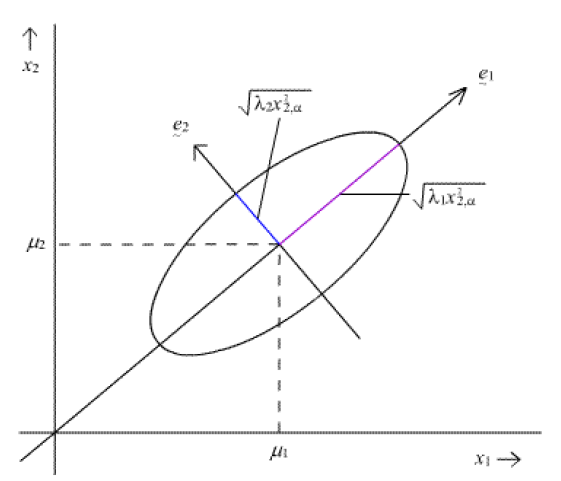
Birçok veri madenciliği probleminde olduğu gibi burada da amaç en az seviyede bilgi kaybı. Eğer bilginin tanımı ne derseniz, bir bakış açısı değişkenler arası ilişkiler der (kovaryans). Kovaryans ile ilgili detaylı bilgiye http://tr.wikipedia.org/wiki/Kovaryans linkinden ulaşabilirsiniz. Amaç eldeki büyük veriyi değişkenler arası ilişkileri en iyi şekilde koruyarak daha küçük bir uzayda ifade etmeye çalışmaktan ibaret (yukarıdaki şekilde gösterildiği gibi). Bunu anlatmak için Gaussian (Normal) dağılımının geometrisinden bahsetmek istiyorum. Yine kolaylık sağlaması adına iki değişkenli (bivariate) bir Gaussian dağılım ele alalım. Gaussian dağılım olasılık yoğunluk fonksiyonu şekli itibariyle elips şeklindeki dağılımlar (http://en.wikipedia.org/wiki/Elliptical_distribution) sınıfına girer ve bu dağılımın parametreleri her değişken için ortalama ve de değişkenler arası ilişkiyi anlatan kovaryans matrisidir. Bu parametreler olasılık yoğunluk fonksiyonun şeklini (yani elipsin) şeklini belirler. Aşağıda buna bir örnek görebilirsiniz.
Bir şekilde değişkenler arası ilişkinin yönünü gösteren e1 ve e2 vektörleri, dağılımın parametresi olan kovaryans matrisinin özvektörleridir (eigenvector). Eğer yukarıda gösterdiğimiz projeksiyonlar ile ilişkilendirirsek, verimizin Gaussian dağıldığını varsayıp örneklerimiz üzerinden hesapladığımız kovaryans matrisinin (örnek [“sample”] kovaryansı) özvektörleri bizim için ideal projeksiyonu vermesini bekleriz. Özvektörlere ait özdeğerler (eigenvalue) ise o yöndeki ilişkinin gücünü verecektir. Bazen bu türden bir ilişkiye sinyal olarak bakıp bu yöndeki sinyallerin gücü olarak da adlandırılır. Peki neden özvektörler derseniz, özvektörlerin birbirine dik olması bir önemli özellik. Böylece projeksiyon yaptığımız zaman birbiriyle korelasyonu sıfır olan iki vektörü kullanmış oluyoruz ve bu da aynı bilgiyi tekrar kullanmamak adına önemli oluyor. Bu türden bir analizde özdeğerler verideki varyansın ne kadarını kapsadığımız hakkında bilgi verir.
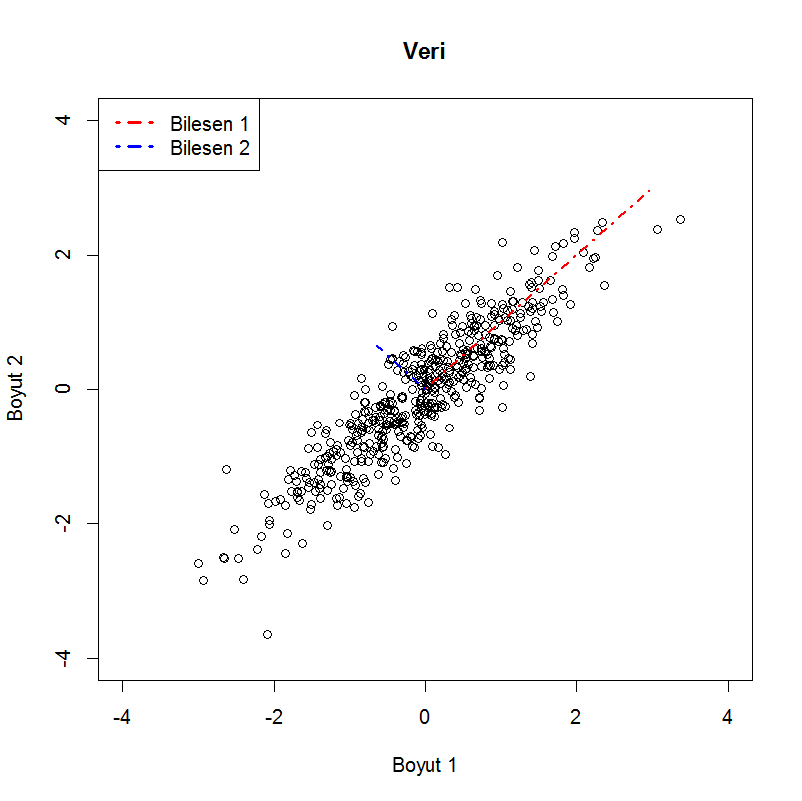
Aşağıdaki şekilde de bunu görebilirsiniz. Verimiz (500 adet Gaussian dağılımdan rastgele yaratılmış nokta) x ekseninde daha uzun, yani o yöndeki ilişkiyi bir şekilde hesaba katmamız önemli. y eksenindeki nispeten bir tür gürültü etkisi var gibi. Bu veri ortalamaları 0 olan ve kovaryans matrisi [latex] \begin{array}{cc} 1 & 0.8 \\ 0.8 & 1 \end{array} [/latex] olan iki değişkenli (bivariate) Gaussian dağılımdan üretildi. TBA sonucu bulunan düzlemler (özvektörler) de özdeğerleri ile doğru orantılı olarak şekilde gösterilmiştir. Burada özdeğeri en yüksek (değişkenliğin daha büyük bir bölümünü açıklayabilen) bileşeni seçip artık 2 değişkenli noktalarımızı tek bir değerle ifade edebiliriz. Bu değer aslında çok basit anlamda birim uzunluktaki özvektör ile veri vektörünün çarpımı. Yani bir izdüşümü. Buna şöyle de bakılabilir. Öyle vektörler bulduk ki, orijinal nokta bu vektörlerin lineer kombinasyonu şeklinde ifade edilebilir. Biz de bu lineer kombinasyonun ağırlıklarını yeni veri olarak kullanabiliriz (çünkü temel (basis) vektörler sabit ve veriler katsayılar cinsinden ifade edilebilir). Bunu bir başka yazıda yüz tanıma problemi üzerinde anlatmaya çalışacağım.
Kovaryans matrisi üzerinde çalıştığımız için değişkenlerin ölçekleri önemlidir. Farklı seviyelerde değişkenler olduğunda her değişkenden (her sütun) ortalaması çıkarılıp daha sonra bu değerler standart sapmaya bölünür. Yani bir tür standardizasyon ya da normalizasyon yapmak gerekir. İkiden fazla değişkenin olduğu ve olçek farklılıkları olduğu durumda değişkenler arası ilişkilerin büyüklüğü (kovaryans matrisinin elemanları) karşılaştırılabilir olmaktan çıkar.
Modifiye edilmemiş haliyle TBA verinizin Gaussian bir dağılımdan geldiğini ve lineer ilişkileri barındırdığını varsayar. Bu varsayımları aşmak için alternatif yöntemler ve TBA üzerinde çeşitlemeler (örnegin kernel PCA) önerilmiştir. Bilgisayar bilimlerinde bunu bir tür veri sıkıştırma yöntemi olarak da anlatırlar. Çünkü p boyutundaki verinizi artık daha küçük bir uzayda (ya da daha az değişkenle) ve minimal bilgi kaybıyla ifade etmek temel amaçtır.